Tight-Binding Lieb¶

Motivations¶

liebTB is a module providing a Python implementation of a face centered square lattice within the tight-binding framework. It can be used to build up and solve tight-binding models with complex valued onsite energies and/or hoppings. As such, this package can be used to analyze the concepts of Parity-Time symmetry, Parity-Time symmetry breaking, zero-modes, and topologically protection.

The lattice is defined by:

three sublattices named A, B and C. The unit cell is given by:

four hoppings:

In the $x$ direction: the intradimer coupling $t_{ab}$ which links the A sites to the B sites, and the interdimer hopping $t_{ba}$ which links the B sites to the A sites.

In the $y$ direction: the intradimer coupling $t_{ac}$ which links the A sites to the B sites, and the interdimer hopping $t_{ca}$ which links the C sites to the A sites.

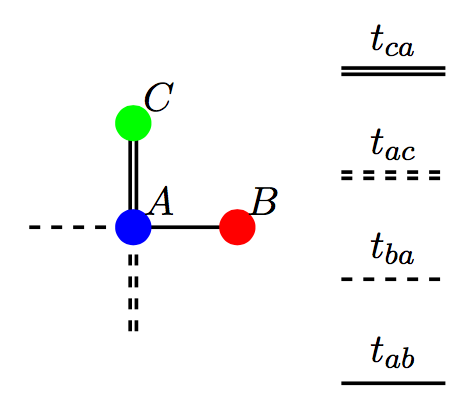
liebTB can

obtain the spectrum (eigenenergies of the tight-binding Hamiltonian) and the probability densities of the states of the system (absolute value squared eigenvectors of the Hamiltonian).

obtain the polarization of the A sublattice (the sum of the probability densities of the A sites)

select states by introducing a condition on the A sublattice polarization (revealing zero modes and/or localized states).

test the robustness to disorder by implementing hopping disorder.

get the time evolution of the field (using the Crank-Nicolson method).

get the time evolution of the field with adiabatic pumping (smooth variation of the hoppings).

Installation¶

liebTB is available at https://github.com/cpoli/TB

To use liebTB, you need to install the programming language python and three additional packages:

python 3.x

numpy

scipy

matplotlib

See https://cpoli.github.io/python-doc.html for details, and the TB module https://github.com/cpoli/TB:

latticeTB

eigTB

plotTB

propTB

Feedback¶

Please send comments or suggestions for improvement to cpoli83 at hotmail dot fr