About¶

This is the primary site for the distribution of the python package graphene_flake, from Charles Poli at Lancaster University.

Motivations¶

The graphene_flake package models a tight-binding graphene flake submited to inhomogeneous triaxial linear strain [Sch13], [Pol14].

The lattice is defined by two sublattices labeled A and B, and three hoppings: 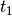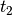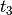$t_1$ , $t_2$ , $t_3$ , and three bond vectors : $\rho_1$ , $\rho_2$ , $\rho_3$ .

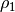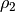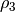In presence of the triaxial linear train, the hoppings are given by:

$t_l = t [1 + (\beta/2)\boldsymbol{\rho}_l . \mathbf{r}_l]\, , \quad \text{with}, l=1,2, 3.$

The resulting strain-induced hopping pattern:

The class graphene_flake can

obtain the spectrum (eigenenergies of the tight-binding Hamiltonian) and the probability densities of the states of the system (modulus squared eigenvectors of the Hamiltonian).

select states by introducing a condition on the eigenenergies.

Analyze the degeneracy and the wavefunction support of the pLLs.

Analyze the evolution of the eigenenergies depending on the strength of the strain (analogous to the Hofstadter’s butterfly).

Analyze the vortex-induced localized states appearing between pLLs.

References¶

[Sch13]

H. Schomerus, Parity Anomaly and Landau-Level Lasing in Strained Photonic Honeycomb Lattices. Phys. Rev. Lett. 110, 013903 (2013)

[Pol14]

C. Poli, J. Arkinstall, and H. Schomerus, Degeneracy doubling and sublattice polarization in strain-induced pseudo-Landau levels. Phys. Rev. B 90, 155418 (2014).

Feedback¶

Please send comments or suggestions for improvement to cpoli83 at hotmail dot fr